データ構造
■ 木構造。
基本的なデータ構造の1つ。データ同士の階層関係を表す。
1つのデータから複数のデータに分岐していく構造になっている。
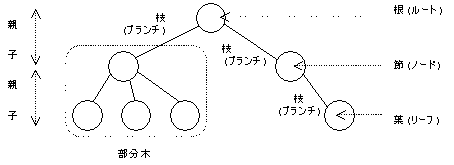
木構造において、各要素を節(ノード)、それを結ぶ線を枝(ブランチ)と呼ぶ。
また、最上位の節を根(ルート)、最下位の節を葉(リーフ)という。
隣接要素の上下関係は、親、子と呼ぶ。
 ■ 完全2分木
すべての枝の分岐が2つ以下である木のことを、2分木という。
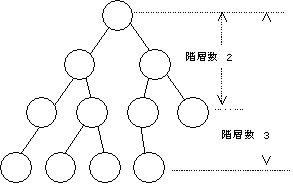
2分木の中でも、特に根からすべての葉にいたる階層数が
等しくなっているような2分木を、完全2分木と呼ぶ。
一般には、階層数の差が1以下の場合を含めて、完全2分木と呼ぶ。
■ 完全2分木
すべての枝の分岐が2つ以下である木のことを、2分木という。
2分木の中でも、特に根からすべての葉にいたる階層数が
等しくなっているような2分木を、完全2分木と呼ぶ。
一般には、階層数の差が1以下の場合を含めて、完全2分木と呼ぶ。
 ■ 2分探索木。
2分木の各節に探索キーを与えて探索を可能としたもの。
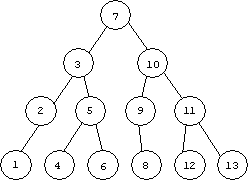
2分探索木では、左部分木と右部分木をたばねる節に対して、
両部分木が持つキーの中間のキーを割り当てる。
データを検索する場合には、
節ごとのキーと探索対象データのキーとの大小を比較し、
検索対象が左にあるか、右にあるかを絞り込む。
なお、最も効率的な2分探索木は、完全2分木である。
■ 2分探索木。
2分木の各節に探索キーを与えて探索を可能としたもの。
2分探索木では、左部分木と右部分木をたばねる節に対して、
両部分木が持つキーの中間のキーを割り当てる。
データを検索する場合には、
節ごとのキーと探索対象データのキーとの大小を比較し、
検索対象が左にあるか、右にあるかを絞り込む。
なお、最も効率的な2分探索木は、完全2分木である。
 ■ ヒープ。
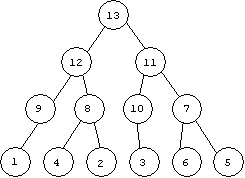
親節のキーと子節のキーの大小関係が、つねに一致している完全2分木。
ヒープには、親>子の場合と、親<子の場合の2種類がある。
前者の場合は、根のキーが最大値、葉のキーが最小値となる。
後者の場合は、根のキーが最小値、葉のキーが最大値となる。
■ ヒープ。
親節のキーと子節のキーの大小関係が、つねに一致している完全2分木。
ヒープには、親>子の場合と、親<子の場合の2種類がある。
前者の場合は、根のキーが最大値、葉のキーが最小値となる。
後者の場合は、根のキーが最小値、葉のキーが最大値となる。
 ■ スタック。Stack。
データの挿入や削除の操作を、リストの片側だけで可能にしたデータ構造。
最後に格納したデータは、データを取り出すとき、一番最初に取り出される。
すなわち、後入れ先出し(LIFO:Last In First Out)の性質を持つ。
スタックは、コンピュータの中で、サブルーチンが呼ぶ出されたとき、
戻りアドレスを記憶しておくのに利用する。
スタックを利用することで、サブルーチンが入れ子になる再帰手続きにおいても、
正確に元のアドレスに戻ることができる。
なお、スタックにデータを追加する操作をプッシュ(Push)といい、
逆にスタックからデータを取り出す操作をポップ(Pop)という。
■ キュー。Queue。
データの挿入が片側だけから行われ、
データの削除がもう一方だけで行われるデータ構造。
最初に格納されたデータが、最初に処理される。
すなわち先入れ先出し(FIFO:First In First Out)の性質を持つ。
待ち行列は、コンピュータの中で、先着順に処理すべきあらゆる場面で使われる。
例えば、マルチタスク環境で、複数のタスクにCPU時間を割りあてる際に
使用されている。
なお、待ち行列にデータを追加する操作をエンキュー(Enqueue)といい、
逆にデータを取り出す操作をデキュー(Dequeue)という。
以上。
2004/03/10 pm
■ スタック。Stack。
データの挿入や削除の操作を、リストの片側だけで可能にしたデータ構造。
最後に格納したデータは、データを取り出すとき、一番最初に取り出される。
すなわち、後入れ先出し(LIFO:Last In First Out)の性質を持つ。
スタックは、コンピュータの中で、サブルーチンが呼ぶ出されたとき、
戻りアドレスを記憶しておくのに利用する。
スタックを利用することで、サブルーチンが入れ子になる再帰手続きにおいても、
正確に元のアドレスに戻ることができる。
なお、スタックにデータを追加する操作をプッシュ(Push)といい、
逆にスタックからデータを取り出す操作をポップ(Pop)という。
■ キュー。Queue。
データの挿入が片側だけから行われ、
データの削除がもう一方だけで行われるデータ構造。
最初に格納されたデータが、最初に処理される。
すなわち先入れ先出し(FIFO:First In First Out)の性質を持つ。
待ち行列は、コンピュータの中で、先着順に処理すべきあらゆる場面で使われる。
例えば、マルチタスク環境で、複数のタスクにCPU時間を割りあてる際に
使用されている。
なお、待ち行列にデータを追加する操作をエンキュー(Enqueue)といい、
逆にデータを取り出す操作をデキュー(Dequeue)という。
以上。
2004/03/10 pm
HOME |
BACK
 ■ 完全2分木
すべての枝の分岐が2つ以下である木のことを、2分木という。
2分木の中でも、特に根からすべての葉にいたる階層数が
等しくなっているような2分木を、完全2分木と呼ぶ。
一般には、階層数の差が1以下の場合を含めて、完全2分木と呼ぶ。
■ 完全2分木
すべての枝の分岐が2つ以下である木のことを、2分木という。
2分木の中でも、特に根からすべての葉にいたる階層数が
等しくなっているような2分木を、完全2分木と呼ぶ。
一般には、階層数の差が1以下の場合を含めて、完全2分木と呼ぶ。
 ■ 2分探索木。
2分木の各節に探索キーを与えて探索を可能としたもの。
2分探索木では、左部分木と右部分木をたばねる節に対して、
両部分木が持つキーの中間のキーを割り当てる。
データを検索する場合には、
節ごとのキーと探索対象データのキーとの大小を比較し、
検索対象が左にあるか、右にあるかを絞り込む。
なお、最も効率的な2分探索木は、完全2分木である。
■ 2分探索木。
2分木の各節に探索キーを与えて探索を可能としたもの。
2分探索木では、左部分木と右部分木をたばねる節に対して、
両部分木が持つキーの中間のキーを割り当てる。
データを検索する場合には、
節ごとのキーと探索対象データのキーとの大小を比較し、
検索対象が左にあるか、右にあるかを絞り込む。
なお、最も効率的な2分探索木は、完全2分木である。
 ■ ヒープ。
親節のキーと子節のキーの大小関係が、つねに一致している完全2分木。
ヒープには、親>子の場合と、親<子の場合の2種類がある。
前者の場合は、根のキーが最大値、葉のキーが最小値となる。
後者の場合は、根のキーが最小値、葉のキーが最大値となる。
■ ヒープ。
親節のキーと子節のキーの大小関係が、つねに一致している完全2分木。
ヒープには、親>子の場合と、親<子の場合の2種類がある。
前者の場合は、根のキーが最大値、葉のキーが最小値となる。
後者の場合は、根のキーが最小値、葉のキーが最大値となる。
 ■ スタック。Stack。
データの挿入や削除の操作を、リストの片側だけで可能にしたデータ構造。
最後に格納したデータは、データを取り出すとき、一番最初に取り出される。
すなわち、後入れ先出し(LIFO:Last In First Out)の性質を持つ。
スタックは、コンピュータの中で、サブルーチンが呼ぶ出されたとき、
戻りアドレスを記憶しておくのに利用する。
スタックを利用することで、サブルーチンが入れ子になる再帰手続きにおいても、
正確に元のアドレスに戻ることができる。
なお、スタックにデータを追加する操作をプッシュ(Push)といい、
逆にスタックからデータを取り出す操作をポップ(Pop)という。
■ キュー。Queue。
データの挿入が片側だけから行われ、
データの削除がもう一方だけで行われるデータ構造。
最初に格納されたデータが、最初に処理される。
すなわち先入れ先出し(FIFO:First In First Out)の性質を持つ。
待ち行列は、コンピュータの中で、先着順に処理すべきあらゆる場面で使われる。
例えば、マルチタスク環境で、複数のタスクにCPU時間を割りあてる際に
使用されている。
なお、待ち行列にデータを追加する操作をエンキュー(Enqueue)といい、
逆にデータを取り出す操作をデキュー(Dequeue)という。
以上。
2004/03/10 pm
■ スタック。Stack。
データの挿入や削除の操作を、リストの片側だけで可能にしたデータ構造。
最後に格納したデータは、データを取り出すとき、一番最初に取り出される。
すなわち、後入れ先出し(LIFO:Last In First Out)の性質を持つ。
スタックは、コンピュータの中で、サブルーチンが呼ぶ出されたとき、
戻りアドレスを記憶しておくのに利用する。
スタックを利用することで、サブルーチンが入れ子になる再帰手続きにおいても、
正確に元のアドレスに戻ることができる。
なお、スタックにデータを追加する操作をプッシュ(Push)といい、
逆にスタックからデータを取り出す操作をポップ(Pop)という。
■ キュー。Queue。
データの挿入が片側だけから行われ、
データの削除がもう一方だけで行われるデータ構造。
最初に格納されたデータが、最初に処理される。
すなわち先入れ先出し(FIFO:First In First Out)の性質を持つ。
待ち行列は、コンピュータの中で、先着順に処理すべきあらゆる場面で使われる。
例えば、マルチタスク環境で、複数のタスクにCPU時間を割りあてる際に
使用されている。
なお、待ち行列にデータを追加する操作をエンキュー(Enqueue)といい、
逆にデータを取り出す操作をデキュー(Dequeue)という。
以上。
2004/03/10 pm