待ち行列

■ 待ち行列。Queue。

  母集団からのシステムに対する要求が、
  窓口の処理能力をオーバーした場合に発生する。
  この待ち行列と、次に示す母集団、窓口の関係を
  理論的に表現したものを待ち行列モデルと言う。

  待ち行列理論では、
  システムに対するサービスを要求している集団を母集団と呼ぶ。
  ネットワークシステムでは、トランザクションの発生源を指す。

  また、母集団からの要求に対し、それを実行するところを、窓口と呼ぶ。
  具体的には、システム全体、もしくは回線、CPU、磁気ディスクなどの諸要素が
  相当する。

■ ポアソン到着。

  トランザクションが時間的にランダムに発生するとき、
  単位時間中に発生するトランザクションの個数は、ポアソン分布に従う。
  ここでトランザクションの窓口への到着が、ポアソン分布に従い、
  かつ下記の仮定を満たすとき、これをポアソン到着と呼ぶ。

  (1)独立性

    あるトランザクションの到着は過去の事象と無関係であり、
    次のトランザクションの発生に影響を与えない。

  (2)希少性

    ごく短い時間に、2つ以上のトランザクションが同時に到着することは、
    無視できるほど少ない。

  (3)定常性

    ある時間に対し、トランザクションの到着する確率は、
    どの時間帯を取っても同じである。

■ M/M/1モデル。

  待ち行列モデルの表記法。
  ケンドールは、待ち行列モデルを、
  トランザクションの到着間隔の確率分布、窓口のサービス時間の確率分布、
  窓口数の3つの観点で捉え、A/B/n形式で表した。

  このケンドール表記で表される
  最も代表的な待ち行列モデルは、M/M/1モデルである。
  M/M/1とは、トランザクションの到着間隔がランダムで、
  サービス時間が指数分布、窓口数が1つであることを表す。

  ほかにも、窓口が複数になるM/M/nモデルなどがある。

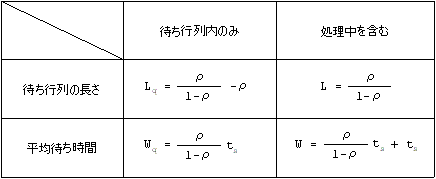
■ M/M/1モデルの公式のまとめ。

   

■ 平均到着率。

  単位時間当たりに何個のトランザクションが到着するか、を表す。
  トランザクションの平均到着率は、トランザクションの平均到着間隔taの逆数である。

  λ=1/ta (a=arrival)

■ 平均サービス率。

  窓口が、単位時間当たりに処理可能なトランザクションの数を表す。
  窓口の平均サービス率は、窓口の平均サービス時間tsの逆数である。

  μ=1/ts (s=service)

■ 利用率。

  窓口がどれだけ利用されているか、の度合いを表す値。

  利用率は、トランザクションの平均到着率λと
  窓口の平均サービス率μの割合で求められる。
  システム設計においては常に、λ<μでなければならない。

  利用率 ρ=λ/μ (0<ρ<1)

  利用率はまた、トランザクションの平均到着間隔taと
  窓口の平均サービス時間tsの割合に等しい。
  システム設計においては常に、taa/ts (0<ρ<1)

■ 待ち行列の長さ。

  処理中のトランザクションを含めて、
  現時点でシステム内にあるすべてのトランザクションの個数Lは、
  次式で求められる。ここで、0<ρ<1である。

  L = ρ/(1-ρ) 

  処理中のトランザクションを除き、
  現時点で待ち行列内で待っているトランザクションの個数Lqは、
  次式で求められる。ここで、0<ρ<1である。

  Lq = ρ/(1-ρ)-ρ = ρ2/(1-ρ) 

■ 平均待ち時間。

  トランザクションが自分の処理が始まるまで、
  待ち行列の中で待つ平均待ち時間Wqは、次式で求められる。

  Wq = ρ/(1-ρ)×ts

  トランザクションが自分の処理が終わるまでに、
  システムの中で待つ平均応答時間Wは、次式で求められる。

  W = ρ/(1-ρ)×ts +ts = 1/(1-ρ)×ts

■ 2個のM/M/1と1個のM/M/2の比較。

  トランザクションが2倍に急増した場合には、
  M/M/1を2本設ける方法よりも、M/M/2を1本設ける方法がより有利である。

  M/M/1を2本設けた場合、2個の窓口に対して2個の待ち行列ができる。
  窓口のサービス時間は変わらず、到着率も変わらない。
  このため、利用率も変わらない。
  平均待ち時間ρ/(1-ρ)×tsも従来と同じである。

  M/M/2を1本設けた場合、2個の窓口に1つの待ち行列ができる。
  窓口のサービス時間は事実上半分になり、到着率は2倍になる。
  このため、利用率は変わらない。
  しかし平均待ち時間ρ/(1-ρ)×tsでは、半分になる。

以上。

2004/03/12 pm