その他のば自ステイルメイト 解答
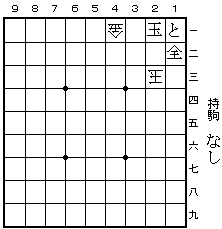
第1問 (2001年1月13日)
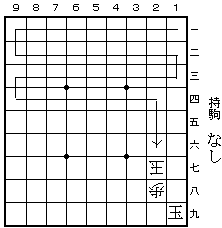 21と 同玉 31龍 同玉 41龍 同玉 51馬 同玉 61馬 同玉
71金 同玉 81金 同玉 91香成 同玉 92金 同玉 82金 同玉
72全 同玉 62全 同玉 52全 同玉 42全 同玉 32と 同玉
22と 同玉 12香成 同玉 13圭 同玉 23圭 同玉 33圭 同玉
43圭 同玉 53杏 同玉 63と 同玉 73と 同玉 83と 同玉
93香成 同玉 94と 同玉 84と 同玉 74と 同玉 64と 同玉
54と 同玉 44と 同玉 34と 同玉 24と 同玉 25と 同玉
26歩 同玉 27と 同玉 まで 74手。
21と 同玉 31龍 同玉 41龍 同玉 51馬 同玉 61馬 同玉
71金 同玉 81金 同玉 91香成 同玉 92金 同玉 82金 同玉
72全 同玉 62全 同玉 52全 同玉 42全 同玉 32と 同玉
22と 同玉 12香成 同玉 13圭 同玉 23圭 同玉 33圭 同玉
43圭 同玉 53杏 同玉 63と 同玉 73と 同玉 83と 同玉
93香成 同玉 94と 同玉 84と 同玉 74と 同玉 64と 同玉
54と 同玉 44と 同玉 34と 同玉 24と 同玉 25と 同玉
26歩 同玉 27と 同玉 まで 74手。
→手順再生
最短手数の全駒煙です。それだけ(笑)。玉方の37手はすべて駒取りでなくてはならないので、詰まさないように気を付けて王手をかけていくと自動的に解けます。
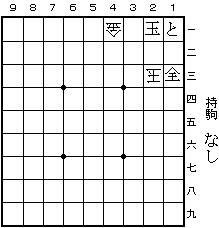
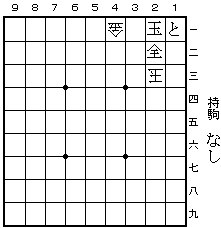
第2問 (2001年1月20日)
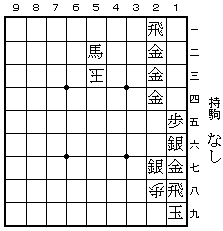 98と 同玉 97と 同玉 96と 同玉 95と 同玉 94と 同玉
84と 同玉 85と 同玉 86と 同玉 87と 同玉 88と 同玉
79と 同玉 78と 同玉 77と 同玉 76と 同玉 75と 同玉
74と 同玉 64杏 同玉 65杏 同玉 66杏 同玉 67杏 同玉
68圭 同玉 58圭 同玉 57圭 同玉 56圭 同玉 55全 同玉
54全 同玉 53角成 同玉 52角成(右図) 同玉 41飛成 同玉 31金 同玉
22金 同玉 13金 同玉 14歩 同玉 25銀 同玉 36銀 同玉
27金 同玉 17飛 同玉 まで 74手。
98と 同玉 97と 同玉 96と 同玉 95と 同玉 94と 同玉
84と 同玉 85と 同玉 86と 同玉 87と 同玉 88と 同玉
79と 同玉 78と 同玉 77と 同玉 76と 同玉 75と 同玉
74と 同玉 64杏 同玉 65杏 同玉 66杏 同玉 67杏 同玉
68圭 同玉 58圭 同玉 57圭 同玉 56圭 同玉 55全 同玉
54全 同玉 53角成 同玉 52角成(右図) 同玉 41飛成 同玉 31金 同玉
22金 同玉 13金 同玉 14歩 同玉 25銀 同玉 36銀 同玉
27金 同玉 17飛 同玉 まで 74手。
→手順再生
これも最短手数の全駒煙です。後半捨て方が少し複雑になりますが、前問と同じです。3筋には駒を置かず、左は成駒、右は生駒という無意味な趣向があります。
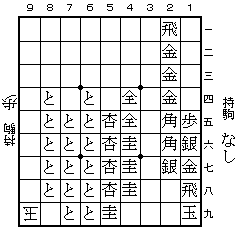
…というのが普通の答えですが、それは真の解ではありません。
考えてみて下さい。問題図が実戦から生じた局面だとして、一手前の手は何でしょうか?28歩?違います。もし、一手前の手が 28歩 だったとすると、一手前は右図のようだったことになります。さらに一手前は何でしょうか。何であったとしても、その前の後手の手は指す手がなくなってしまいます。
ですから、問題図一手前の手は 28歩 ではありません。しかし、他に可能性があるでしょうか?
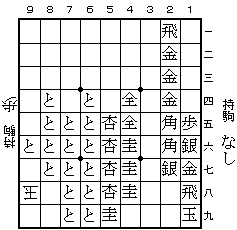
右図を見て下さい。ここから、 97と引 99玉 88と引 28歩 87と左 で問題図となります。おわかりいただけたでしょうか。問題図は先手番ではなく後手番でしかあり得ないのです。したがって、「ば自ステイルメイト?手」の真の解は、「29歩成 同玉 まで 2手」です。怒ってはいけません。これは「華麗な詰将棋」の第一問で若島正氏が使ったアイディアです。
ちなみに、問題図が先手番でないようにするためには2筋が一段目まで埋まっていることが必要です。そのため、駒の配置には苦心しました。
第3問 (2001年2月5日)
 23銀 33玉 22銀生 23玉 13銀成(下左図) 33玉
23全 42玉 32全 43玉 42全 33玉 32全 23玉
22全(下右図) 13玉 12全 23玉 13全(下左図) 33玉
23全 42玉 32全 43玉 42全 33玉 32全 23玉
22全(下右図) 13玉 12全 23玉 13全(下左図) 33玉
23全 42玉 32全 43玉 42全 33玉 32全 23玉
22全(下右図) 13玉 12全 23玉 まで 46手。
23銀 33玉 22銀生 23玉 13銀成(下左図) 33玉
23全 42玉 32全 43玉 42全 33玉 32全 23玉
22全(下右図) 13玉 12全 23玉 13全(下左図) 33玉
23全 42玉 32全 43玉 42全 33玉 32全 23玉
22全(下右図) 13玉 12全 23玉 13全(下左図) 33玉
23全 42玉 32全 43玉 42全 33玉 32全 23玉
22全(下右図) 13玉 12全 23玉 まで 46手。
→手順再生
初手から、23銀 同玉 としたいところですが、残念ながら 12と という手が残っています。しかし、先手に飛び道具がなく合駒を出現させることのできないこの状況では、12とを防止することはできないように思われます。
困難を打破するのが、千日手を利用するというアイディアです。上記の手順のように進めてみましょう。詰め上がりの局面において、先手に残された手は 13全 と 22全 です。ところが、13全 なら4度目の左上図が出現することになり、22全 なら4度目の右上図が出現することになります。これは、どちらも連続王手の千日手ですから禁手です。(千日手は「同一局面4回」で成立することに注意して下さい。)したがって、詰め上がりでは先手に可能な手が残っていないことになります。念のため、詰め上がりの局面までに、4回出現している局面がないことをご確認下さい。
(補足)
「問題図に至る以前に上図のような局面がすでに出現してしまっている可能性はないのか?」ということを気にされる方がいらっしゃるかもしれません。もしそう聞かれたら「ないとは言えません、すみません。」と答えるしかないのですが、それを気にしだすとどんな詰将棋も成立しなくなってしまうということで、お茶を濁したいと思います。
第4問 (2001年3月26日)
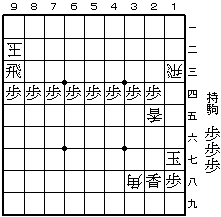 29香 28角 同香 25香 24歩 33玉 34歩 43玉 44歩 53玉
54歩 63玉 64歩 72玉 94角 83飛 同角生 38角 74歩 83玉
84歩 93玉 94歩 92玉 93飛 13飛 まで26手(3歩余り)。
29香 28角 同香 25香 24歩 33玉 34歩 43玉 44歩 53玉
54歩 63玉 64歩 72玉 94角 83飛 同角生 38角 74歩 83玉
84歩 93玉 94歩 92玉 93飛 13飛 まで26手(3歩余り)。
→手順再生
駒余りだが、ば自ステイルメイトにおいては駒余りの方が珍しいので、あえてこれで完全と主張したい。なお、持ち歩を二枚減らすと次のような余詰が生じる。
29香 28飛 同香 26香 24歩 同玉 25歩 同玉 24飛 15玉
14飛 94飛 84歩 同飛 74歩 同飛 64歩 同飛 54歩 同飛
44歩 同飛 34歩 同飛 24歩 同飛 まで26手。
2005年8月8日追記:持ち歩を一枚減らすと次のような余詰が生じる(神無太郎さん指摘)。このため、持ち歩を1枚増やしました。
24歩 同玉 25歩 33玉 34歩 同玉 35歩 同玉 36歩 25玉
29香 28飛 同香 26香 35飛 95飛 85歩 同飛 75歩 同飛
65歩 同飛 55歩 同飛 45歩 同飛 まで 26手
第5問 (2001年12月27日)
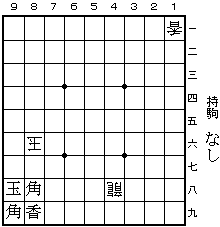 19角 28香 同角/11香 75玉 39角 48香 同角 86玉 89香 28龍/88角
99角 48龍/88角 まで12手。
19角 28香 同角/11香 75玉 39角 48香 同角 86玉 89香 28龍/88角
99角 48龍/88角 まで12手。
9手目 89香 に 28龍/88角 のように攻方駒の復活を利用して王手を防ぐ手法は「魔女返し」と呼ばれている。ここでは、魔女返しを2度続けるのが狙い。
2002年2月6日追記 : fmで検討できるようになったので検討したところ、やはり余詰がありました。
82角 53玉 71角 同龍/88角 97角 86歩 同角/83歩 44玉 99角 88香 77角 同龍 まで12手です。
2004年1月13日追記 : fmでの検討はまだですが、修正案を考えたので記しておきます。キルケ 98王+飛角2香,62玉 12手。82飛 73玉 28角 37飛 84飛成 同玉 39角打 57飛打 89香 39飛成/88角 99角 28龍/88角 まで12手。
第6問 (2003年5月3日)
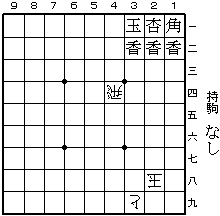 11角 44飛 59飛 46玉 49飛 48香 同飛 37玉 38香 28玉
32香生 38香 同飛 27玉 29香 28香 同香 18玉/29桂 21香成 27玉
28香 18玉 22香生 29玉 28飛 同玉 まで26手。
11角 44飛 59飛 46玉 49飛 48香 同飛 37玉 38香 28玉
32香生 38香 同飛 27玉 29香 28香 同香 18玉/29桂 21香成 27玉
28香 18玉 22香生 29玉 28飛 同玉 まで26手。
→手順再生
27歩 18桂を盤上から消す必要があるため、玉が上部に移動する余裕がない。飛と香の連携でうまくブロックを作って、自王の動きをなくす。
この構想はキルケと直接関連していないが、ただのば自ステイルメイトではどうやっても早詰になってしまう。このようにキルケを導入しても、双方ともに自由度が高いため完全かどうか自信はない。fmでの検討はできていないため、余詰があるかもしれない。
2004年1月13日追記 : やはり余詰がありました。11角 22金 51飛 52飛 同飛成/82飛 45玉 42龍 同飛/28飛 48飛 36玉 38飛 27玉 37飛 18玉/29桂 38飛 29玉 28飛 同玉 まで 18手(神無七郎さん指摘)。どうもありがとうございました。修正は無理そうですが、このまま置いておきます。
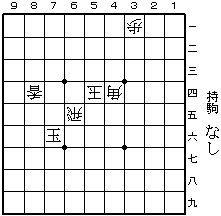
第7問 (2004年1月13日)
2解ということで、二つの手順でステイルメイトにできます。
解その1:
▲2五銀 △同玉 ▲9五飛 △6五飛 ▲3四銀 △同玉
▲9四飛 △4四角 ▲4三銀 △同玉 ▲9三飛成 △8三香
▲5四銀 △同玉 ▲8四龍 △同香 まで16手。(詰め上がり図は左下)
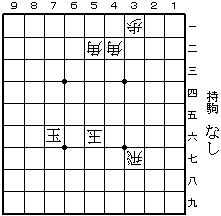
解その2:
▲2七銀 △同玉 ▲2二飛 △2五角 ▲3八銀 △同玉
▲3二飛成 △3七飛 ▲4七銀 △同玉 ▲4一龍 △4二角
▲5六銀 △同玉 ▲5二龍 △同角 まで16手。(詰め上がり図は右下)
→手順再生 その1
→手順再生 その2
2004年(平成16年)の年賀詰(のようなもの)として掲示板上でひっそりと出題してみた。といっても、どこをとっても年賀詰らしくないので、普通に出した方がよかったかもしれない。
詰将棋パラダイス2003年8月号(誤植のため9月号で修正再出題)の森茂氏作の双裸玉ば自ステイルメイト(14王+飛銀4,34玉 16手)に着想を得て創作した。手順は全く異なるのに持駒と手数を合わせたのは、森氏に敬意を表する意味を込めたため。
2つの手順は左からと上からということで対称性のある方だと思うが、3一の歩が余詰防止にしか役立っていないのは大きな減点事項。ここに掲載するのでなければ、1解目の頭2手を削って14手1解にするところだろう。それなら双裸玉で完全になる。
- このページの問題
- 双裸玉ば自ステイルメイト集
 21と 同玉 31龍 同玉 41龍 同玉 51馬 同玉 61馬 同玉
71金 同玉 81金 同玉 91香成 同玉 92金 同玉 82金 同玉
72全 同玉 62全 同玉 52全 同玉 42全 同玉 32と 同玉
22と 同玉 12香成 同玉 13圭 同玉 23圭 同玉 33圭 同玉
43圭 同玉 53杏 同玉 63と 同玉 73と 同玉 83と 同玉
93香成 同玉 94と 同玉 84と 同玉 74と 同玉 64と 同玉
54と 同玉 44と 同玉 34と 同玉 24と 同玉 25と 同玉
26歩 同玉 27と 同玉 まで 74手。
21と 同玉 31龍 同玉 41龍 同玉 51馬 同玉 61馬 同玉
71金 同玉 81金 同玉 91香成 同玉 92金 同玉 82金 同玉
72全 同玉 62全 同玉 52全 同玉 42全 同玉 32と 同玉
22と 同玉 12香成 同玉 13圭 同玉 23圭 同玉 33圭 同玉
43圭 同玉 53杏 同玉 63と 同玉 73と 同玉 83と 同玉
93香成 同玉 94と 同玉 84と 同玉 74と 同玉 64と 同玉
54と 同玉 44と 同玉 34と 同玉 24と 同玉 25と 同玉
26歩 同玉 27と 同玉 まで 74手。
 98と 同玉 97と 同玉 96と 同玉 95と 同玉 94と 同玉
84と 同玉 85と 同玉 86と 同玉 87と 同玉 88と 同玉
79と 同玉 78と 同玉 77と 同玉 76と 同玉 75と 同玉
74と 同玉 64杏 同玉 65杏 同玉 66杏 同玉 67杏 同玉
68圭 同玉 58圭 同玉 57圭 同玉 56圭 同玉 55全 同玉
54全 同玉 53角成 同玉 52角成(右図) 同玉 41飛成 同玉 31金 同玉
22金 同玉 13金 同玉 14歩 同玉 25銀 同玉 36銀 同玉
27金 同玉 17飛 同玉 まで 74手。
98と 同玉 97と 同玉 96と 同玉 95と 同玉 94と 同玉
84と 同玉 85と 同玉 86と 同玉 87と 同玉 88と 同玉
79と 同玉 78と 同玉 77と 同玉 76と 同玉 75と 同玉
74と 同玉 64杏 同玉 65杏 同玉 66杏 同玉 67杏 同玉
68圭 同玉 58圭 同玉 57圭 同玉 56圭 同玉 55全 同玉
54全 同玉 53角成 同玉 52角成(右図) 同玉 41飛成 同玉 31金 同玉
22金 同玉 13金 同玉 14歩 同玉 25銀 同玉 36銀 同玉
27金 同玉 17飛 同玉 まで 74手。


 23銀 33玉 22銀生 23玉 13銀成(下左図) 33玉
23全 42玉 32全 43玉 42全 33玉 32全 23玉
22全(下右図) 13玉 12全 23玉 13全(下左図) 33玉
23全 42玉 32全 43玉 42全 33玉 32全 23玉
22全(下右図) 13玉 12全 23玉 13全(下左図) 33玉
23全 42玉 32全 43玉 42全 33玉 32全 23玉
22全(下右図) 13玉 12全 23玉 まで 46手。
23銀 33玉 22銀生 23玉 13銀成(下左図) 33玉
23全 42玉 32全 43玉 42全 33玉 32全 23玉
22全(下右図) 13玉 12全 23玉 13全(下左図) 33玉
23全 42玉 32全 43玉 42全 33玉 32全 23玉
22全(下右図) 13玉 12全 23玉 13全(下左図) 33玉
23全 42玉 32全 43玉 42全 33玉 32全 23玉
22全(下右図) 13玉 12全 23玉 まで 46手。


 29香 28角 同香 25香 24歩 33玉 34歩 43玉 44歩 53玉
54歩 63玉 64歩 72玉 94角 83飛 同角生 38角 74歩 83玉
84歩 93玉 94歩 92玉 93飛 13飛 まで26手(3歩余り)。
29香 28角 同香 25香 24歩 33玉 34歩 43玉 44歩 53玉
54歩 63玉 64歩 72玉 94角 83飛 同角生 38角 74歩 83玉
84歩 93玉 94歩 92玉 93飛 13飛 まで26手(3歩余り)。 19角 28香 同角/11香 75玉 39角 48香 同角 86玉 89香 28龍/88角
99角 48龍/88角 まで12手。
19角 28香 同角/11香 75玉 39角 48香 同角 86玉 89香 28龍/88角
99角 48龍/88角 まで12手。
 11角 44飛 59飛 46玉 49飛 48香 同飛 37玉 38香 28玉
32香生 38香 同飛 27玉 29香 28香 同香 18玉/29桂 21香成 27玉
28香 18玉 22香生 29玉 28飛 同玉 まで26手。
11角 44飛 59飛 46玉 49飛 48香 同飛 37玉 38香 28玉
32香生 38香 同飛 27玉 29香 28香 同香 18玉/29桂 21香成 27玉
28香 18玉 22香生 29玉 28飛 同玉 まで26手。

